Théorie des nombres
Sur les sommes de carrés 11 pages, télécharger en PDF.
Théorème de la progression arithmétique de Dirichlet 16 pages, télécharger en PDF.
Test de Lucas (primalité des nombres de Mersenne) 2 pages, télécharger en PDF.
Théorème de Wolstenhome 1 page, télécharger en PDF.
Introduction à la Théorie Algébrique des Nombres 80 pages, télécharger en PDF
Ce papier contient une démonstration du théorème des deux carrés ainsi d'une condition pour assurer l'unicité d'une telle décomposition (admise), trois démonstrations du critère pour qu'un nombre premier soit somme de deux carrés (deux accessibles en terminale S, l'autre, classique, utilisant l'anneau des entiers de Gauss). Je démontre aussi le théorème des quatre carrés avec des moyens très élémentaires (bac +1). Enfin on trouvera l'énoncé d'un critère pour savoir si un nombre est somme de trois carrés ou pas ; seule la condition suffisante est prouvée.
Depuis Euclide, on sait qu'il existe une infinité de nombres premiers. Naturellement, on peut se demander si étant donnés a et b premiers entre eux, il existe une infinité de nombres premiers de la forme an+b (si a et b ne sont pas premiers entre eux, il est clair qu'aucun des nombres an+b ne sera premier).
Euler résolut de façon purement algébrique la question dans le cas des nombres de la forme an+1. La démonstration de cette proposition fera l'objet de la première section de ce papier. Plus tard, en 1835, Dirichlet démontra le théorème dans toute sa généralité, par des méthodes analytiques. La preuve classique passe par l'analyse complexe ; nous présentons ici une variante utilisant l'analyse réelle, tirée d'un article de Robin Chapman. Auparavant, il nous faudra prouver quelques résultats de théorie des groupes et des propriétés élémentaires sur la fonction zeta de Riemann.
On donne une condition nécessaire et suffisante sur un entier de la forme 2n-1 pour qu'il soit premier. La preuve exposée n'est pas la plus rapide qui soit, mais c'est une belle application de l'algèbre linéaire et de la théorie des groupes.
Une démonstration d'un résultat amusant dû à Wolstenhome, dont voici l'énoncé : Soit p > 3 un nombre premier alors le numérateur de 1 + 1/2 + 1/3 + ... + 1/(p-1) est divisible par p2 . Exemple pour p = 5, on a 1 + 1/2 + 1/3 + 1/4 = 25/12 et le numérateur est bien divisible par p2 = 25.
Cet article propose une introduction à la théorie algébrique des nombres, basée sur l'intégralité. Ayant un goût pour les anneaux principaux et euclidiens, cette notion apparaît en filigrane tout au long du texte.
Dans le premier chapitre, après voir mis en évidence au travers d'un exemple le rôle des idéaux premiers dans un anneau d'entiers non factoriel, je présente les notions de base sur l'intégralité ainsi que les deux exemples essentiels pour la suite, à savoir les entiers quadratiques et cyclotomiques.
Le chapitre 2 traite de la factorisation dans un anneau de Dedekind. J'établis l'existence et l'unicité de la décomposition en produit d'idéaux premiers et donne les rudiments sur les idéaux fractionnaires. Un fait remarquable est qu'il y équivalence entre factorialité et principalité dans ces anneaux.
Dans le chapitre 3, je fais quelques rappel sur la localisation puis j'introduis la notion de norme d'idéaux. Elle s'avère utile pour étudier le sujet qui occupe ce chapitre, la factorisation dans les extensions. Le cas galoisien est agréable, il servira ici à étudier les entiers cyclotomiques. Dans le cas d'un anneau d'entiers monogène, la factorisation des idéaux engendrés par un nombre premier p et liée à celle du polynôme minimal modulo p de l'élément monogène. Ce résultat s'avère utile pour l'étude à la main des groupes de classes d'idéaux. On démontre au passage la loi de réciprocité quadratique.
Les groupes de classes d'idéaux sont l'objet du chapitre 4. Je démontre par deux méthodes la finitude de ceux-ci. L'une très simple, basée sur le principe des tiroirs, l'autre basée sur le théorème de Minkowski sur les réseaux. La borne obtenue est bien meilleure en vue des calculs explicites de groupes de classes qui vont suivre, notamment celui de 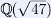 . Enfin je montre que
. Enfin je montre que  (où
(où  est une racine primitive 23-ième de l'unité) n'est pas principal ; je mentionne un théorème de Masley qui donne de façon exhaustive les corps cyclotomiques dont le nombre de classes est un entier compris entre 1 et 10.
est une racine primitive 23-ième de l'unité) n'est pas principal ; je mentionne un théorème de Masley qui donne de façon exhaustive les corps cyclotomiques dont le nombre de classes est un entier compris entre 1 et 10.
Le chapitre 5 traite exclusivement des corps quadratiques imaginaires. Je donne une méthode algorithmique pour calculer un groupe de classes d'un tel corps basé sur le groupe modulaire. Si l'on ne s'intéresse qu'au nombre de classes, il existe un résultat frappant qui dit que ce nombre est égal aux nombre de classes de formes quadratiques binaires définies positives ayant pour discriminant le discriminant du corps quadratique en question... Il en résulte un algorithme très simple pour effectuer ce calcul.
Stark en 1967 a déterminé de façon exhaustive les corps quadratiques imaginaires principaux, ils sont au nombre de 9. Il n'est pas question ici de prouver ce résultat compliqué, je me contente de démontrer une version très faible de ce théorème ; c'est l'occasion d'utiliser les résultats sur la factorisation dans les extensions exposés au chapitre 3, ainsi que la loi de réciprocité quadratique.
Enfin je présente la résolution de deux équations diophantiennes : l'équation de Mordell (y2=x3+d, avec d entier) et l'équation de Fermat pour l'exposant 3. On y voit apparaître toute la force de l'existence et l'unicité de la factorisation en produit d'idéaux premiers.
Le chapitre 6 porte sur les anneaux d'entiers euclidiens. Le problème est riche en questions non résolues. Après avoir abordé le cas des entiers quadratiques imaginaires pour lequel tout est connu, je dis un mot du cas réel qui recèle encore des mystères. La liste exhaustive de ces anneaux qui sont euclidiens pour la norme est connu, mais dans cette liste ne figure pas certains (on pourrait dire : presque tous) anneaux principaux. C'est le cas 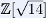 pour lequel Pierre Samuel avait posé la question : cet anneau pourrait-il être euclidien pour un autre stathme ? En 2000, Harper a démontré que c'est effectivement le cas.
pour lequel Pierre Samuel avait posé la question : cet anneau pourrait-il être euclidien pour un autre stathme ? En 2000, Harper a démontré que c'est effectivement le cas.
J'aborde ensuite le cas des entiers cyclotomiques, en montrant que le 5ème corps cyclotomique est euclidien pour la norme. Je donne un panorama de la recherche sur le sujet, avec là encore des points d'interrogation qui subsistent. Citons par exemple un théorème dû à Harper (2004) qui affirme qu'il y équivalence entre euclidiennité et principalité dans ces anneaux, donc en particulier (théorème de Masley), l'anneau des entiers de 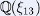 est euclidien. Mais jusqu'à aujourd'hui, personne n'a réussi à prouver si la norme est un stathme ou pas pour cet annneau.
est euclidien. Mais jusqu'à aujourd'hui, personne n'a réussi à prouver si la norme est un stathme ou pas pour cet annneau.
Pour finir, je consacre deux pages à quelques résultats récents d'Harper allant dans le sens d'un résultat de Weilberger qui affirme que sous l'hypothèse de Riemann généralisée, dans un anneau d'entiers qui a une infinité d'unités, il y a équivalence entre euclidiennité et principalité. Ces hypothèses sont notamment satisfaites dans les anneaux d'entiers quadratiques réels.