Géométrie
- Théorème de Lehmus-Steiner généralisé.
11 pages, télécharger en PDF.
On s’intéresse dans ce papier à la recherche de conditions nécessaires et suffisantes pour que les bissectrices, intérieures ou extérieures, issues de deux sommets d’un triangle triangle aient la même longueur.
Le cas de deux bissectrices intérieures est bien connu, c’est le théorème de Steiner-Lehmus qui affirme qu’il est nécessaire et suffisant que le triangle considéré soit isocèle. Ce résultat a été démontré par Steiner en 1842 après que Lehmus lui eut envoyé une lettre demandant une preuve géométrique.
Lorsque l’une des bissectrices est extérieure, on obtient une belle CNS portant sur les angles. On développora deux preuves de ce résultat, l’une algébrique en exprimant les longueurs des bissectrices en fonction de celle des côtés, l’autre trigonométrique en les exprimant en fonction des angles. On en déduira des expressions des éléments du triangle en fonction de paramètres bien choisis. On donnera également des exemples simples de tels triangles.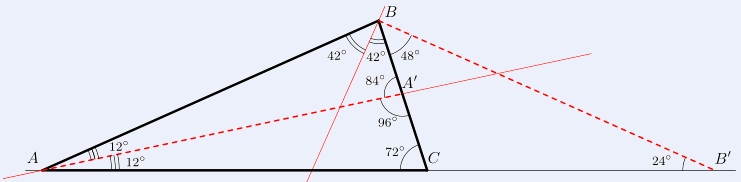 Un exemple de triangle dans lequel une bissectrice intérieure a la même longueur qu'une bissectrice extérieure (représentées en pointillé rouge)
Un exemple de triangle dans lequel une bissectrice intérieure a la même longueur qu'une bissectrice extérieure (représentées en pointillé rouge) - Sur les quadrilatères inscriptibles. 5 pages, télécharger en PDF.
Voici une version préliminaire de l'article que j'ai publié dans le numéro de Quadrature de juillet-septembre 2004 en collaboration avec Norbert Verdier. On trouvera notamment deux preuves de l'inégalité de Ptolémée, ainsi qu'une preuve de la fameuse formule de Brahmagupta qui exprime l'aire d'un quadralitère inscriptible en fonction de la longueur de ses côtés.